На уроках информатики, изучая тему «История вычислительной техники», упоминается устройство логарифмическая линейка. Что это такое? Как она выглядит? Как ей пользоваться? Рассмотрим историю создания данного устройства и принцип работы.

Логарифмическая линейка — это счетный прибор, применявшийся до появления калькуляторов и персональных компьютеров. Это было достаточно универсальное устройство, на котором можно было умножать, делить, возводить в квадрат и куб, вычислять квадратные и  кубические корни, синусы, тангенсы и другие значения. Выполнялись эти математические операции с достаточно большой точностью — до 3–4 знаков после запятой.

История логарифмической линейки

В 1622 году Уильям Отред (William Oughtred 5 марта 1575—30 июня 1660) создает, пожалуй, один из самых успешных аналоговых вычислительных механизмов — логарифмическую линейку. Отред является одним из создателей современной математической символики — автор нескольких стандартных в современной математике обозначений и знаков операций:

• Знак умножения — косой крестик: ×
• Знак деления — косая черта: /
• Символ параллельности: ||
• Краткие обозначения функций sin и cos (раньше писали полностью: Sinus, Cosinus)
• Термин «кубическое уравнение».

«Все его мысли были сосредоточены на математике, и он все время размышлял или чертил линии и фигуры на земле… Его дом был полон юных джентльменов, которые приезжали отовсюду, чтобы поучиться у него».

Неизвестный современник Отреда

Отред внёс решающий вклад в изобретение удобной для пользования логарифмической линейки тем, что предложил использовать две одинаковые шкалы, скользящие одна вдоль другой. Саму идею логарифмической шкалы ранее опубликовал валлиец Эдмунд Гюнтер, но для выполнения вычислений эту шкалу нужно было тщательно измерять двумя циркулями.

Логарифмическая шкала

Гюнтер ввел также общепринятое теперь обозначение log и термины косинус и котангенс. В 1620 году вышла книга Гюнтера, где дано описание его логарифмической шкалы, а также помещены таблицы логарифмов, синусов и котангенсов. Что же касается самого логарифма, то его изобрел, как известно, шотландец Джон Непер. Видя недоумение Форстера, высоко ценившего данное изобретение, Отред показал своему ученику два изготовленных им вычислительных инструмента — две логарифмические линейки.

Логарифмическая шкала Гюнтера являлась прародителем логарифмической линейки и подвергалась многократным доработкам. Так в 1624 году Эдмунд Уингейт издал книгу, в которой описал модификацию шкалы Гюнтера, позволяющую легко возводить числа в квадрат и в куб, а также извлекать квадратные и кубические корни.

Дальнейшие усовершенствования привели к созданию логарифмической линейки, однако, авторство этого изобретения оспаривают два ученых Уильям Отред и Ричард Деламейн.

Первая линейка Отреда имела две логарифмические шкалы, одна из которых могла смещаться относительно другой, неподвижной. Второй инструмент представлял собой кольцо, внутри которого вращался на оси круг. На круге (снаружи) и внутри кольца были изображены “свернутые в окружность” логарифмические шкалы. Обе линейки позволяли обходиться без циркулей.

Логарифическая линейка Отреда

В 1632 году в Лондоне вышла книга Отреда и Форстера “Круги пропорций” с описанием круговой логарифмической линейки (уже иной конструкции), а описание прямоугольной логарифмической линейки Отреда дано в книге Форстера “Дополнение к использованию инструмента, называемого “Кругами пропорций”, вышедшей в следующем году.

Линейка Ричарда Деламейна (который был в свое время ассистентом Отреда), описанная им в брошюре “Граммелогия, или Математическое кольцо”, появившейся в 1630 году, тоже представляла собой кольцо, внутри которого вращался круг. Потом эта брошюра с изменениями и дополнениями издавалась еще несколько раз. Деламейн описал несколько вариантов таких линеек (содержащих до 13 шкал). В специальном углублении Деламейн поместил плоский указатель, способный двигаться вдоль радиуса, что облегчало использование линейки. Предлагались и другие конструкции. Деламейн не только представил описания линеек, но и дал методику градуировки, предложил способы проверки точности и привел примеры использования своих устройств.

А в 1654 году англичанин Роберт Биссакер предложил конструкцию прямоугольной логарифмической линейки, общий вид которой сохранился до нашего времени…

В 1850 году девятнадцатилетний французский офицер Амедей Маннхейм создал прямоугольную логарифмическую линейку, ставшую прообразом современных линеек и обеспечивающую точность до трех десятичных знаков. Этот инструмент он описал в книге «Модифицированная вычислительная линейка», изданной в 1851 году. В течение 20-30 лет эта модель выпускалась только во Франции, а затем ее стали изготавливать в Англии, Германии и США. Вскоре линейка Маннхейма завоевала популярность во всем мире.

Логарифмическая линейка долгие годы оставалась самым массовым и доступным прибором индивидуального вычисления, несмотря на бурное развитие вычислительных машин. Естественно, она обладала небольшой точностью и скоростью решения по сравнению с вычислительными машинами, однако, на практике большинство исходных данных были не точные, а приближенные величины, определенные с той или иной степенью точности. А, как известно, результаты вычислений с приближенными числами будут всегда приближенные. Этот факт и высокая стоимость вычислительной техники позволили Логарифмической линейке просуществовать практически до конца 20 столетия.

Логарифмическая линейка

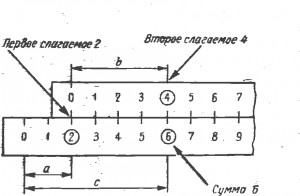
Сложение

2 + 4 = 6

Сложение с помощью логарифмической линейки

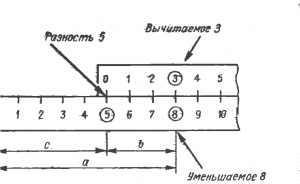
Вычитание

8 – 3 = 5

Вычитание с помощью логарифмической линейки

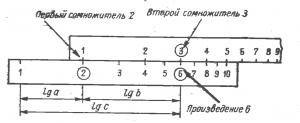
Умножение

a ∙ b = с при a = 2, b = 3

Логарифмируя обе части равенства, имеем: Lg(a) + lg(b )= lg(с).

Взяв две линейки с логарифмическими шкалами, видим, что сложение значений lg2 и lg3 дает в результате lg6, то есть произведение 2 на 3.

Умножение с помощью логарифмической линейки

На основной шкале корпуса линейки (вторая снизу) выбирается первый сомножитель и на него устанавливается начало основной, нижней, шкалы  движка (она на лицевой стороне последнего и точно такая же, как основная шкала корпуса).

На основной шкале движка волосок бегунка устанавливается на втором сомножителе.

Ответ находится на основной шкале корпуса линейки под волоском. Если при этом волосок выходит за пределы шкалы, то на первый сомножитель устанавливают не начало, а конец движка (с числом 10).

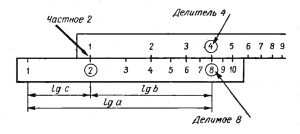
Деление

a/b = с при a = 8, b = 4

Логарифмируя обе части равенства, получим: Lg(a) – lg(b) = lg(с).

Разность логарифмов делимого и делителя дает логарифм частного,  в нашем случае — 2.

Деление с помощью логарифмической линейки

На основной шкале корпуса линейки выбирается делимое, на которое  устанавливается волосок бегунка.

Под волосок подводится делитель, найденный на основной шкале движка.  Результат определяется на основной шкале корпуса напротив начала или конца движка.

Возведение в степень и извлечение корня

Шкала квадратов чисел — вторая сверху, кубов — первая сверху.

Волосок устанавливается на возводимом числе на основной шкале корпуса,  а под волоском на соответствующей шкале считывается результат.

При извлечении квадратного и кубического корней, наоборот, результат находится на основной шкале.

Перенос при расчетах с запятой

Если, например, один из сомножителей равен 126, то на линейке используется значение 1,26, а найденное произведение увеличивается в 100 раз. При возведении в куб числа 0,375 результат, найденный для числа 3,75, уменьшается в 1000 раз и т.п.