Закончился школьный тур Всероссийской олимпиады школьников. Разберем первую и вторую задачи тура, проводимого в московских школах. Для написания программ будет использоваться Python 3.

Задача №1. Улица.

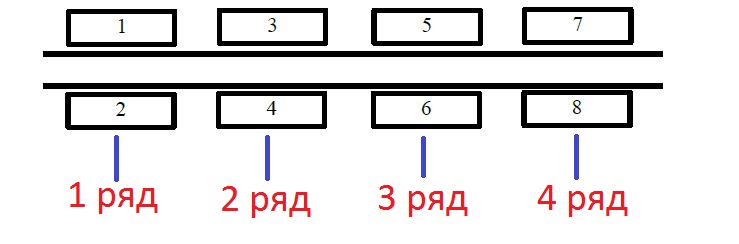
По одну сторону улицы находятся дома с нечётными номерами (1, 3, 5, …), по другую сторону – с чётными (2, 4, 6, …). Дом № 1 находится напротив дома № 2, дом № 3 – напротив дома № 4 и т. д. До соседнего дома нужно идти вдоль по улице одну минуту, неважно, с какой стороны улицы он находится (то есть от дома № 1 нужно идти одну минуту как до дома № 3, так и до дома № 4). До дома, стоящего напротив, идти не нужно.

Человек вышел на улицу из дома номер A и должен дойти до дома номер B.
Определите, сколько минут ему нужно идти вдоль по улице.
Программа получает на вход два различных целых положительных числа A и B, не превосходящие 2×10⁹, – номера домов. Программа должна вывести одно число – искомое
количество минут.

Пример входных и выходных данных:

Ввод
1
8

Вывод
3

Решение.

Задача сводится к нахождению времени, которое человек тратит на прохождение от одного ряда домов к другому. Так как время прохождения между соседними рядами равно 1 минуте, достаточно найти расстояние между рядами, на которых находятся интересующие нас дома.

1 ряд —  1 и 2 дома

2 ряд — 3 — 4 дома

и т.д.

Остается написать алгоритм, который бы определял, на каком ряду находится данный дом.

Заметим, что

• 2 дом на 1 ряду
• 4 дом на 2 ряду
• 6 дом на 3 ряду и т.д.

Т.е. четный номер дома n находится на n / 2 ряду

Теперь определимся с нечетными номерами домов:

• 1 дом на 1 ряду
• 3 дом на 2 ряду
• 5 дом на 3 ряду и т.д.

Нетрудно увидеть, что нечетный номер дома ряд находятся на  (n + 1) / 2 ряду.

Напишем программу, определяющую, на каком ряду находится дом с введенным номером

a = int(input()) #вводим номер дома, из которого вышел человек
b = int(input()) #вводим номер дома, до которого должен дойти человек
# для каждого номера определяем номер ряда, на котором он находится
if a % 2 == 0:
    n1 = a / 2
else:
    n1 = (a + 1) / 2
if b % 2 == 0: 
    n2 = b / 2 
else: 
    n2 = (b + 1) / 2

Теперь осталось найти расстояние между n1 и n2

Так как человек мог выйти из дома с большим номером в дом с меньшим номером, используем модуль
Выводим ответ

print(abs(n1-n2))

В таком виде ответ будет выводится в формате вещественного числа
Преобразуем в целочисленный тип

print(int(abs(n1-n2)))

Конечный вид программы:

 
a = int(input()) #вводим номер дома, из которого вышел человек 
b = int(input()) #вводим номер дома, до которого должен дойти человек # для каждого номера определяем номер ряда, на котором он находится 
if a % 2 == 0: 
    n1 = a / 2 
else: 
    n1 = (a + 1) / 2
if b % 2 == 0: 
    n2 = b / 2 
else: 
    n2 = (b + 1) / 2
print(int(abs(n1-n2)))

Замечание: определение номера ряда дома можно оформить в виде функции

Задача №2. Надежное крепление.

Уличный рекламный щит прикреплён к опоре при помощи трёх креплений. Первое крепление может выдерживать ветер, скорость которого не превосходит A м/c, второе крепление – B м/c, третье – C м/с. Сам щит будет надёжно закреплён, если как минимум два крепления из трёх выдерживают ветер данной скорости. Определите максимальную скорость ветра, которую выдержит данный щит.
Программа получает на вход три целых положительных числа A, B, С, не превосходящие 2×10⁹, – допустимые скорости ветра, которые выдерживают три крепления щита. Программа должна вывести одно число – максимальную скорость ветра, которую выдержит щит.

Пример входных и выходных данных

Ввод

28
15
10

Вывод

15

Решение.

Каждая пара болтов  будет выдерживать максимальную скорость ветра, равную минимальному значению из двух.

Например:

• Болт А — 28 м/c
• Болт В — 15 м/с

Максимальный ветер, который выдержат данные болты  — 15 м/с

• Болт А — 28 м/c
• Болт С — 10 м/с

Максимальный ветер, который выдержат данные болты  — 10 м/с

• Болт B — 15 м/c
• Болт С — 10 м/с

Максимальный ветер, который выдержат данные болты  — 10 м/с

Таким образом максимальное значение скорости ветра, которую выдержит рекламная конструкция, будет равно максимальному из трех полученных ранее чисел 10, 10, 15.

Получили 15 м/с.

Действительно, при сочетании болта B c болтами А и В, ветер 15 м/c выдержит и та, и другая пара. Это значение скорости ветра будет максимальным.

Программа получается очень короткая. Используем встроенные функции языка Python min() и max()

a = int(input())
b = int(input())
c = int(input())
print(max(min(a, b),min(b, c), min(a, c)))