Вот и закончился школьный тур Всероссийской олимпиады школьников. Как мне показалось, задания были несколько сложнее, чем в прошлом году. В данной статье хотелось бы представить свое решение задачи №3 «Не про спиннеры». Для написания текста программы буду использовать язык Python 3.
Задача.
Саша совсем не любит спиннеры, поэтому он рисует в тетрадке. Он взял тетрадный лист из N × M клеточек и пронумеровал все клетки различными числами. Теперь ему стало
интересно, сколько различных прямоугольников он может вырезать из этого листа бумаги по границам клеточек.
Программа получает на вход два числа N и M – размеры исходного листа. Все числа – целые положительные, не превосходящие 75000.
Программа должна вывести одно число – количество прямоугольников, которые можно вырезать из данного листа бумаги (весь лист целиком также считается одним из возможных прямоугольников).
Решение.
Шаг 1.
Рассмотрим размер исходного листа 3 × 1 (три клетки по горизонтали и одна клетка по вертикали). Как в образце.
Чтобы понять принцип подсчета различных прямоугольников, которые можно вырезать из данного листа, обратимся к следующей схеме:
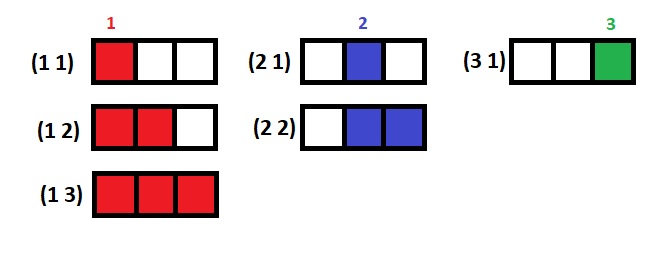
- Обозначим каждую клетку прямоугольника цифрой от 1 до 3.
- Парами чисел (1 1), (1 2), (1 3), (2 1), (2 2) (3 1) обозначим возможные вырезанные прямоугольники. Первая цифра обозначает начало такого прямоугольника, вторая цифра — количество клеток слева направо. Итого получаем 6 различных прямоугольников. Как в таблице с примерами входных и выходных данных.
Из рисунка видно, что ни один из прямоугольников не повторяется.
В первом столбце — 3 варианта, во втором — 2, в третьем — 1.
Таким образом, чтобы посчитать количество различных прямоугольников на листе размера 1 × n (n — натуральное число) необходимо: 1 + 2 + 3 + … + n
Реализовать такой алгоритм довольно просто:
#вводим количество клеток в строке
n = int(input())
# переменная, которая ведет подсчет количества прямоугольников в строке
c = 0
for j in range(1, n + 1):
c = c + j
Шаг 2
Теперь рассмотрим вариант листа вида m × n. Например: 3 × 3.
Мы знаем, что в строке 1 × 3 ровно 1 + 2 + 3 = 6 произвольных прямоугольников.
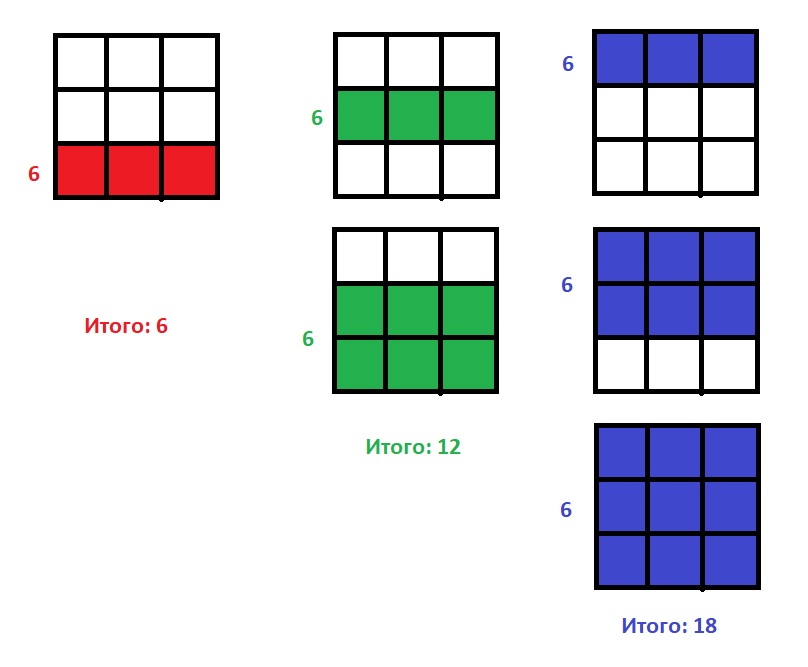
Начнем рассматривать прямоугольник 3 × 3 снизу вверх, делая следующие рассуждения:
Случаи, когда мы берем полоску клеток 2 × 3 или 3 × 3 ничем не отличается от случая 1 × 3 и имеет столько же решений.
Таким образом: 6 + 6 * 2 + 6 * 3 — формула подсчета количества различных прямоугольников на листе 3 × 3.
Напишем полный текст программы с комментариями:
#количество столбцов
n = int(input())
# подсчет прямоугольников в строке
c = 0
# подсчет прямоугольников на листе (итог)
r = 0
# количество строк
m = int(input())
#подсчет количества пр-ов в строке
for j in range(1, n + 1):
c = c + j
#итого прямоугольников
for i in range(1, m + 1):
r = r + c*i
# вывод ответа на экран
print(r)
Думаю, решение выглядит довольно просто.
Есть другие варианты решения задачи — пишите в комментариях на сайте или в группе в Контакте. Было бы интересно!



 8 ноября, 2017
8 ноября, 2017  Andrey K
Andrey K 
 (9 голос, значение: 4,00 из 5)
(9 голос, значение: 4,00 из 5)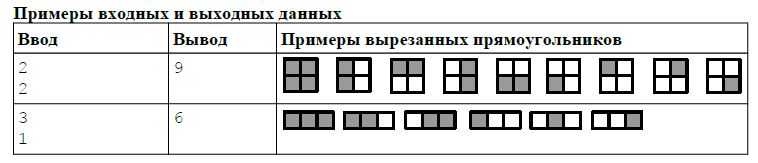
 Опубликовано в рубрике
Опубликовано в рубрике  Метки:
Метки: 