В прошлый раз мы разобрали первые две задачи школьного тура Всероссийской олимпиады школьников, проводимой в Москве. В этот раз мы разберём оставшиеся три задачи. Если вы решили задачу более простым способом — не стесняйтесь, пишите своё решение в комментариях.
Задача №3. Парад
В параде принимают участие M военных. Командование парада решило, что наиболее эффектное построение военных – в форме квадрата, то есть число участников построения должно быть точным квадратом. Но поскольку число M может не быть точным квадратом, разрешается разбить военных на несколько полков, каждый из которых строится в форме квадрата. Для красоты все полки должны быть одинакового размера, также командование парада хочет, чтобы размер каждого полка был как можно больше. Определите максимально возможный размер полка.
Программа получает на вход одно целое положительное число M, не превосходящее 2×109, – количество участников парад. Программа должна вывести одно число – максимально возможный размер полка.
Пример входных и выходных данных:
Ввод
180
Вывод
36
Решение
Исходя из примера входных и выходных данных видим, что 180 человек можно разделить на 5 полков по 36 человек каждый, где 36 — квадрат числа 6 (62 = 36).
Причем любое число M можно представить в виде n * p, где n — количество полков, а p — количество человек в полку (квадрат некоторого числа).
Почему любое? Любое число можно представить как произведение самого себя на единицу, а единица — это квадрат единицы (удовлетворяет условию).
Итак вводимое число будет удовлетворять условию: M = n * p (где p — квадрат некого числа, а n — натуральное число).
Следовательно остаток от деления числа M на p должен быть равен нулю (M % p == 0)
Таким образом необходимо перебрать все числа i, где i2 = p, и M % i2 == 0 . Квадрат самого большого числа из таких i и будет ответом на задачу.
Напишем решение:
m = int(input()) #вводим m
#перебираем все числа i от 1 до m и проверяем на условие
for i in range(1, m + 1):
if m % (i * i) == 0:
p = i ** 2
print(p)
Такое решение будет решать данную задачу, но при больших M время выполнения программы будет высоким, так как мы пробегаемся в цикле по всем i от 1 до m.
Например: для числа 169 максимальным квадратом является само число 169. Для него i =13.
Т.е. для числа 169 целесообразно проверять числа от 1 до квадратного корня это числа — sqrt(169) = 13.
Если квадратный корень не извлекается (как для числа 180), то округляем до целой части сверху.
Итоговый код программы будет такой:
import math
m = int(input())
w = math.floor(math.sqrt(m))
for i in range(1, w + 1):
if m % (i * i) == 0:
p = i ** 2
print(p)
Задача № 4. Ряд чисел
Легенда гласит, что Карл Фридрих Гаусс, учась в школе, смог быстро посчитать сумму целых чисел от 1 до 100, заметив, что 1 + 100 = 2 + 99 = … = 50 + 51. Теперь решите задачу посложнее: можно ли перед каждым из чисел от 1 до N расставить знаки «+» или «–» так, чтобы сумма получившихся чисел была равна 0? Например, для N = 3 сумма –1 –2 +3 будет равна 0, а для N = 2 этого сделать нельзя.
Программа получает на вход целое неотрицательное число N, не превосходящее 105.
Программа должна вывести последовательность из N символов «+» или «–», соответствующих знакам, которые нужно расставить перед числами от 1 до N так, чтобы сумма получившихся чисел была равна 0. Если задача имеет несколько решений, нужно вывести один (любой) ответ. Если задача не имеет решения для данного N, нужно вывести одно слово «IMPOSSIBLE».
Примеры входных и выходных данных:
| Ввод 3 Вывод — — + |
Ввод 2 Вывод IMPOSSIBLE |
Решение
Рассмотрим несколько последовательностей чисел. Заметим, что сумму двух последних чисел в этих последовательностях можно свести к единице или минус единице (1 или -1).
Продолжая рассматривать такие ряды чисел можно заметить, что сумма четырёх последних чисел последовательности (при n >=4) равна нулю.
Если при этом остаются первые 3 числа (1, 2, 3), то из них также можно получить ноль (-1-2+3=0).
Получаем два условия:
- если количество чисел последовательности (или само вводимое число) кратно 4, то ноль получить можно, задавая последовательность знаков -++- каждой четверке чисел.
- если остается три первых числа, то им задаются знаки —+, чтобы в сумме получить ноль.
Во всех остальных случаях получить ноль невозможно.
Напишем программу:
n = int(input())
"""определяем количество 4-ок чисел в последовательности,
дающих ноль
"""
c = n // 4
if n % 4 == 3:
print('--+' + '+--+' * c)
elif n % 4 == 0:
print('+--+' * c)
else:
print('IMPOSSIBLE')
Задача № 5. Клад
Путь к кладу задан в виде указаний, какое количество шагов нужно пройти в одном из четырёх направлений: север (N), юг (S), запад (W), восток (E). Весь маршрут записан в виде строки, содержащей последовательность из чисел и следующих за числами букв, указывающих направление перемещения. Например, строка «7N5E2S3E» означает «пройти 7N5E2S3E» означает шагов на север, 5 шагов на восток, 2 шага на юг, 3 шага на восток». В маршруте может быть много команд перемещения, поэтому каждый такой маршрут можно сократить.
Например, ранее приведённый маршрут можно сократить до 5N8E. По данному маршруту до клада сократите его до строки минимальной длины.
Программа получает на вход строку, состоящую из целых неотрицательных чисел, не превосходящих 107 каждое, и одной буквы («N», «S», «W», «E»). Других символов кроме цифр и букв направлений, в строке нет. Длина строки не превосходит 250 символов. Гарантируется, что начальная и конечная точки маршрута различаются.
Программа должна вывести маршрут, ведущий в ту же точку, записанный в таком же виде, как во входных данных, используя минимальное число символов. Если ответов несколько, программа должна вывести один (любой) из них.
Решение
Необходимо из введенной строки «вытащить» значения шагов и определить направление движения.
Рассмотрим введенную строку слева направо. Будем считывать символы и формировать из них числа, пока не увидим один из символов N, S, E или W:
10N30W20N
ch = ‘1’ + ‘0’
ch = ’10’
Далее переводим получившуюся строку в число («10» в 10).
Возьмем две переменные ns и we: юг-север и восток-запад. Выберем направления, при которых будем прибавлять к переменным ns и we полученные числа, а при которых вычитать.
Пример 1. Для строки 10N30W20N:
ns = 10 + 20 = 30
we = -30
Пример 2. Для строки 10N30W20N35S45E:
ns = 10 + 20 — 35 = -5
we = -30 + 45 = 15
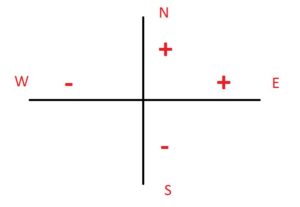
Остается вывести ответ. Если переменная ns оказывается положительным числом — получим 30N (как в первом примере), если отрицательным числом, то получим 5S.
То же самое с переменной we: 30W — в первом примере, 15Е — во втором.
Все зависит от выбранного положительного направлении (смотри рисунок).
Используем условный оператор для реализации данного момента
'N' if ns > 0 else 'S', abs(we), 'E' if we > 0 else 'W'
По условию задачи начальная и конечная точка различны.
Напишем программу, учитывая все вышесказанное
s = input()
svet = ['N','W','E','S']
ch =''
ns = 0
we = 0
for i in range(len(s)):
if s[i] not in svet:
ch += s[i]
else:
if s[i] == 'N':
ns += int(ch)
if s[i] == 'S':
ns -= int(ch)
if s[i] == 'W':
we -= int(ch)
if s[i] == 'E':
we += int(ch)
ch = ''
print(abs(ns), 'N' if ns > 0 else 'S', abs(we), 'E' if we > 0 else 'W', sep='')



 18 ноября, 2018
18 ноября, 2018  Andrey K
Andrey K 
 (14 голос, значение: 4,36 из 5)
(14 голос, значение: 4,36 из 5)
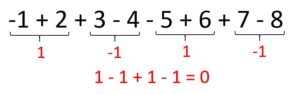
 Опубликовано в рубрике
Опубликовано в рубрике  Метки:
Метки: 
добрый день! хотелось бы скачать информацию
import math
m=int(input())
k=1
for i in range(m):
if math.sqrt(m/k)==round(math.sqrt(m/k)):
print(int(m/k))
break
else:
k+=1